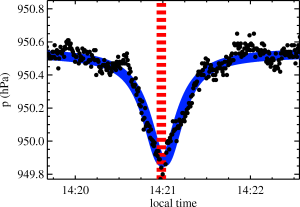
Trying again to dip my toes into advanced data science, I decided to experiment with the Gaussian processes module in sci-kit learn. I’ve been working with barometric data to study dust devils, and that work involves spotting short dips in otherwise slowly varying time series.
In principle, Gaussian processes provides a way to model the slowly varying portion of the time series. Basically, such an analysis assumes the noise infesting each data point depends a little bit on the value of other nearby data points. The technical way to say this is that the covariance matrix for the data stream is non-diagonal.
So I loaded one data file into an ipython notebook and applied the sci-kit learn Gaussian processes module to model out background oscillations. Here’s the notebook.
%matplotlib inline
#2015 Feb 15 -- A lot of this code was adapted from
# http://scikit-learn.org/stable/auto_examples/gaussian_process/plot_gp_regression.html.
import numpy as np
from sklearn.gaussian_process import GaussianProcess
from matplotlib import pyplot as pl
import seaborn as sns
import pandas as pd
sns.set(palette="Set2")
#from numpy import genfromtxt
my_data = np.genfromtxt('Location-A_P28_DATA-003.CSV', delimiter=',', skip_header=7, usecols=(0, 1), names=['time', 'pressure'])
X = np.atleast_2d(np.array(my_data['time'])[0:1000]).T
y = np.atleast_2d(np.array(my_data['pressure'])[0:1000]).T
y -= np.median(y)
# Instanciate a Gaussian Process model
gp = GaussianProcess(theta0=1e-2, thetaL=abs(y[1]-y[0]), thetaU=np.std(y), nugget=1e-3)
# Fit to data using Maximum Likelihood Estimation of the parameters
gp.fit(X, y)
# Make the prediction on the meshed x-axis (ask for MSE as well)
y_pred, MSE = gp.predict(X, eval_MSE=True)
sigma = np.sqrt(MSE)
data = pd.DataFrame(dict(time=X[:,0], pres=y[:,0]))
sns.lmplot("time", "pres", data=data, color='red', fit_reg=False, size=10)
predicted_data = pd.DataFrame(dict(time=X[:,0], pres=y_pred[:,0]))
pl.plot(X, y_pred, color='blue')
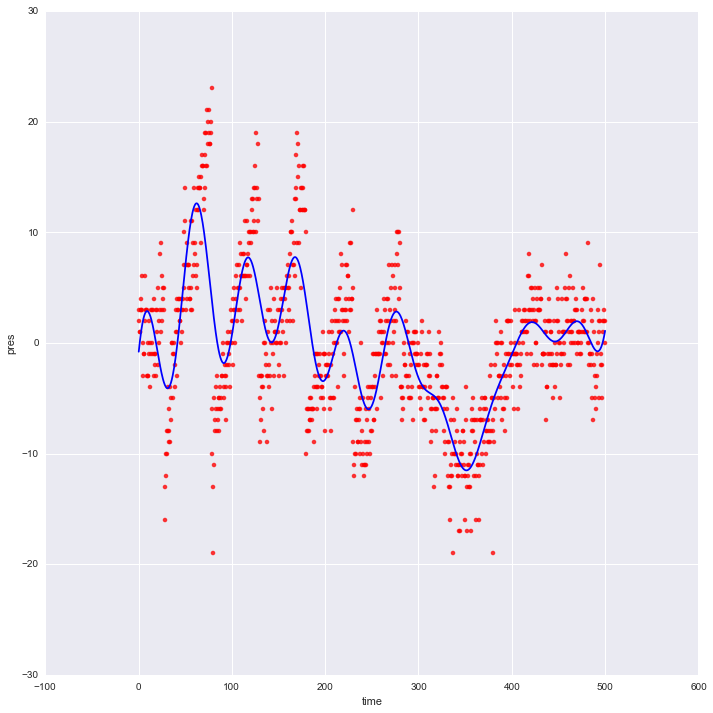
Barometric time series. Pressure in hPa, and time in seconds. The red dots show the original data, and the blue line the fit from the Gaussian process.
Unfortunately, the time series has some large jumps in it, and these are not well described by the slowly varying Gaussian process. What causes these jumps is a good question, but for the purposes of this little analysis, they are a source of trouble.
Probably need to pursue some other technique. Not to mention that the time required to perform a Gaussian process analysis scales with the third power of the number of data points, so it will get very slow very fast.