Animation showing how a machine-learning algorithm decides where lies the boundary between two classes of objects.
Third day of the DPS Meeting was full of fascinating talks about the orbital architectures of exoplanet systems.
One that caught my attention was Dan Tamayo‘s talk on using machine-learning to classify the stability of a planetary system.
As astronomers have discovered more potential planetary systems, it’s becoming more time-consuming to decide whether what we see are actually planets or some other thing that has fooled us into thinking they’re planets.
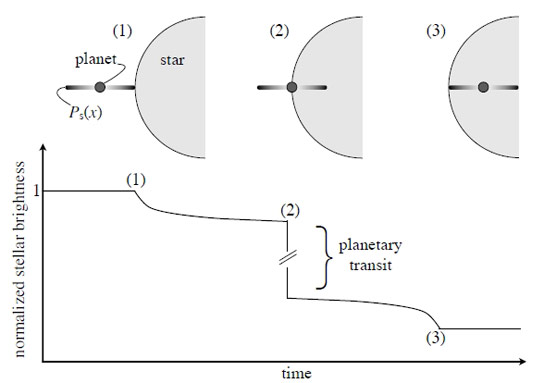
When astronomers find what they think might be a planetary system, one of the first things they check is whether the putative planetary system is actually stable — that is, whether the gravitational tugs among the putative planets would cause the objects to crash into one another or be thrown out of the system.
Since most of the planetary systems we find are probably billions of years, astronomers expect that real planetary systems are stable for billions of years, so if the system we’re looking out turns out to be unstable on short timescales (less than billions of years), we usually decide that it’s not really a planetary system (or that we mis-estimated the planetary parameters).
Unfortunately, doing this check usually requires running big, complicated computer codes, called N-body simulations (“N” for the number of planets or bodies in the system) for hundreds or thousands of computer-hours. That can be a problem if you’ve got planetary candidates flooding in, as with the Kepler or upcoming TESS missions.
Tamayo wanted to try a different approach: what if the same machine-learning techniques that allow Google or Facebook to decide whether someone is likely to buy an iPhone could be used to more quickly decide whether a putative planetary system was stable
So Tamayo created many, many synthetic planetary systems, some stable, some not, and had his machine-learning algorithm sort through them. According to Tamayo, his scheme was able to pick up on subtle features that helped distinguish stable systems from unstable ones with very high accuracy in a fraction of the time it would take to run an N-body simulation.
 I also attended an eye-opening talk from Patricia Knezek of NSF about unconscious biases and their effects in astronomy and planetary science. Knezek explained that several studies have shown how these biases cause everyone to draw unconscious conclusions about someone based on very cursory information, such as their first name, race, gender, etc.
I also attended an eye-opening talk from Patricia Knezek of NSF about unconscious biases and their effects in astronomy and planetary science. Knezek explained that several studies have shown how these biases cause everyone to draw unconscious conclusions about someone based on very cursory information, such as their first name, race, gender, etc.
For instance, one study showed that the same application for a faculty position did much better if the applicant’s first name was “Brian” instead of “Karen”, even when women were evaluating the application.
Fortunately, these same studies have shown several ways to mitigate the effects of these biases, and being aware of them is a big first step.