https://arxiv.org/abs/1910.09523
https://en.wikipedia.org/wiki/Kelvin_wave

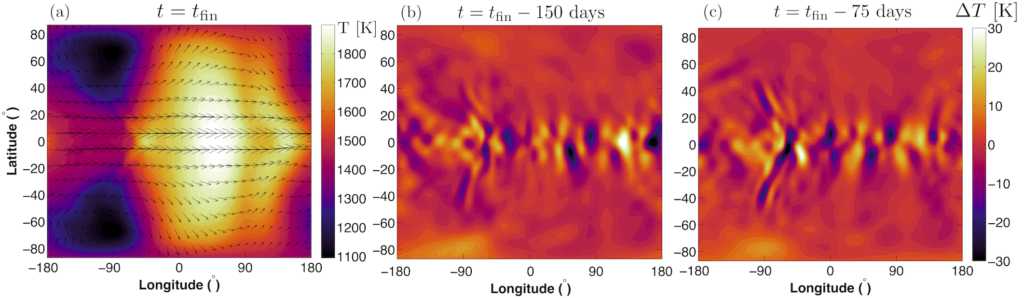
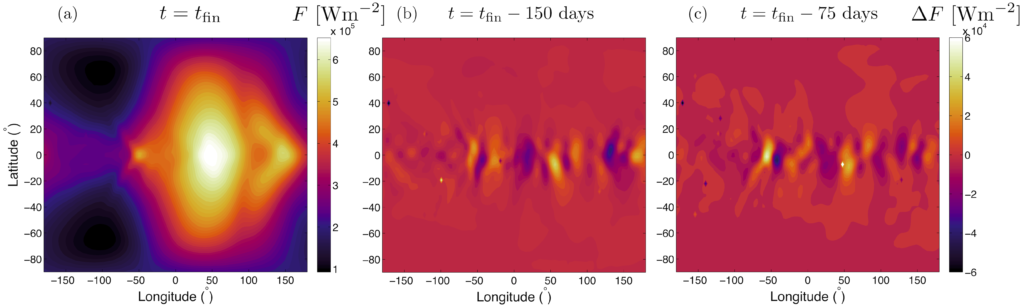
https://arxiv.org/abs/1910.09523
https://en.wikipedia.org/wiki/Kelvin_wave




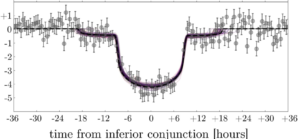
Kepler-1625 b’s transit as seen by Kepler, with the putative moon’s transit appearing as “ears” on either side. From Teachey et al. (2018a).
Last week, Alex Teachey and Dave Kipping of Columbia University presented impressive evidence for what would be the very first known moon orbiting an exoplanet.
The planet, Kepler-1625 b, is likely more massive than Jupiter but in an Earth-like orbit around an old (9 billion years old) but otherwise Sun-like star. Discovered in 2016 among data from the Kepler Mission, the planet was subjected to an intense analysis by Teachey and Kipping as part of the Hunt for Exomoons with Kepler program. In spite of their persistence, Teachey and Kipping found only hints of a moonshadow accompanying the planet’s distinct transit signal.
Hoping to corroborate their putative moon, they applied for and received 40-hours to observe the system with the Hubble Space Telescope (HST) and look for more lunar transits. In these data, Teachey and Kipping found even more convincing evidence for a moon.
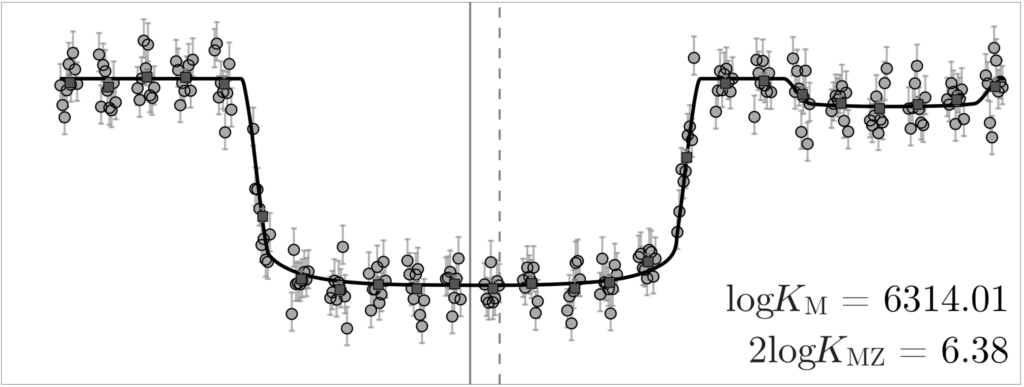
Kepler-1625 b’s and the putative moon’s transits as seen by HST. From Teachey et al. (2018b).
In the figure above, the little dip just to the right of the bigger dip (the planet’s transit) shows every sign of being the shadow of an exomoon circling a star about 7000 lightyears from Earth. Look around at how lucky we are to be alive right now.
Because of the extraordinary magnitude of their claim, Teachey and Kipping peppered their paper with lots of caveats, extending even to their paper’s title (“evidence for an exomoon”, not “we found a large exomoon”).
On top of that, they deployed an flotilla of statistical tests to argue in favor of the exomoon interpretation. One test in particular figures prominently in their analysis – the Bayes factor.
In this context, this ominous-sounding number is a measure of how much more likely one scientific model is over another, given a dataset. For instance, if you found your dog guiltily hiding from a mess in your house (your dataset), you would conclude there is a higher probability your dog made the mess (one scientific model) than a ghost did (another model).

A portrait of someone who may be (but probably isn’t) Thomas Bayes.
The Bayes factor derives from work by the Rev. Thomas Bayes, a minister living in Georgian England, who developed a method to infer the underlying probability for a particular experimental outcome, given results from several actual experiments.
Later, the scientist Simon-Pierre Laplace developed Bayes’ work into a more general theory of inference that he hoped could be used, for example, by juries to judge the guilt or innocence of a defendant.
Nowadays, Bayesian inference shows up everywhere, from analyses of climate change to estimates of the frequency of orange Reese’s pieces. It’s even possible that our brains are natively wired as Bayesian-inference machines.
And so in deciding whether they’d found an exomoon, Teachey and Kipping compared the probability that their Hubble data arose from a model including a lunar transit (as well as gravitational tugs between a planet and moon) to the probability the data showed a lone transiting planet.
Although, as they caution, these probability estimates can’t account for everything, they find the planet-moon model is 400,000 times more probable than the planet-only model.
 As always, more data are needed to corroborate this fantastic result, but if it holds up, Kepler-1625 would be a system with one super-sized Jupiter-like planet accompanied by a Neptune-sized moon which orbits at a distance of about 300,000 km, not too different from our own moon’s distance.
As always, more data are needed to corroborate this fantastic result, but if it holds up, Kepler-1625 would be a system with one super-sized Jupiter-like planet accompanied by a Neptune-sized moon which orbits at a distance of about 300,000 km, not too different from our own moon’s distance.
Very shortly after Teachey and Kipping’s work was published, Kollmeier and Raymond explored the question of whether this monster moon could have its own moon and found that even a moon as large as Ceres could remain stable.
This result immediately prompted a more pressing question: should we call such a body a “sub-moon” or “moonmoon”?
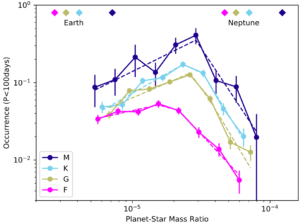
Figure 1: The number of planets per star as a function of the planet-star mass ratio as discovered by Kepler. Dark and light blue curves are for stars less massive than the Sun, while the pink curve is for more massive stars. From Pascucci et al. (2018).
Among the mind-blowing discoveries of the Kepler Mission is that the most common type of planet in the galaxy is the super-Earth/sub-Neptune. This unexpected type of planet straddles the boundary between Earth and Neptune in size and mass, and so they may be super-sized rocky planets or anemic gas-rich planets. We just can’t tell.
Stranger still is that this bizarre chimera orbits one out of every four stars in the Milky Way, but we don’t seem to have one in our solar system (unless the Planet Nine hypothesis pans out).
If that wasn’t enough to make you feel like a planetary outsider, a recent study suggests most planet systems have very different architectures from our own.
In their paper, Prof. Ilaria Pascucci of the University of Arizona and her colleagues studied the distribution of masses for planets discovered by the Kepler Mission. Unlike other recent work, though, they considered not just the planet masses but how they compare to the masses of their parent stars.
Naively, we might expect that more massive stars grow more massive planets, and there is good evidence that more massive stars host more massive dust disks. So as long as the processes that make planets are happy to operate around most any kind of star, then we can use the distribution of planet-star mass ratios to disentangle the influence of stellar mass from other effects.
And Pascucci et al. found exactly what we expected – big stars, small stars, they are all more likely to host planets more massive than Earth — but only up to a point. As shown in Figure 1, the number of planets per star increases with the planet-star mass ratio until it reaches about 0.00003 (or 10 Earth masses for one solar mass) — somewhere between the Earth and Neptune. Above that ratio, the occurrence rate drops, meaning more massive planets are less and less common.
But something even more interesting emerged when Pascucci et al. compared their results based on the Kepler Mission to other surveys. Because Kepler is good at finding planets close to their host stars and not at finding planets farther away, Pascucci’s results don’t tell us much about planets in orbits like Jupiter’s. But microlensing surveys, which use a totally different planet-finding technique, *are* good at finding these more distant planets.
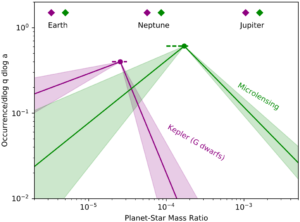
Figure 2: The number of planets around each star with a given planet-star mass ratio for planets close to their host star (as found by Kepler) and planets farther away (as found by microlensing surveys). From Pascucci et al. (2018).
Comparing mass ratios from the two kinds of surveys, Pascucci et al. showed more distant planets found by microlensing also show a preference, but for a ratio several times larger than what’s preferred by closer-in planets — somewhere between Neptune and Jupiter in mass, as shown by the figure above.
What does this all mean? Apparently, the universe seems to like make planets about ten thousand times less massive than their host stars, whether the stars are tiny red dwarfs or massive F-stars. And the farther away the planet is from its star, the more likely it is to be more massive.
Standard planet formation theory predicts this trend: protoplanetary disks (from which planets form) have more solid, icy material farther from the host star, and more solids means more planet.
But these results also make our solar system look even stranger than before. In most solar systems, orbits like Earth’s (and closer) are occupied by planets somewhere between Earth and Neptune in mass, and more distant orbits like Jupiter’s are occupied by planets between Neptune and Jupiter.
It’s tempting to speculate that things that make the solar system unique in one way (in this case, the type of planets we have) are related to other unique things (like, the fact that there’s life here). We don’t know much about super-Earths, but if they turn out to be more Neptune- than Earth-like, it’s not hard to imagine they wouldn’t be good places for life to get started.
Life as we know it needs a planet with a solid surface and lots of liquid water, and so maybe it’s not surprising we haven’t found life elsewhere in the galaxy yet: most of the planets are lifeless, gas balls.
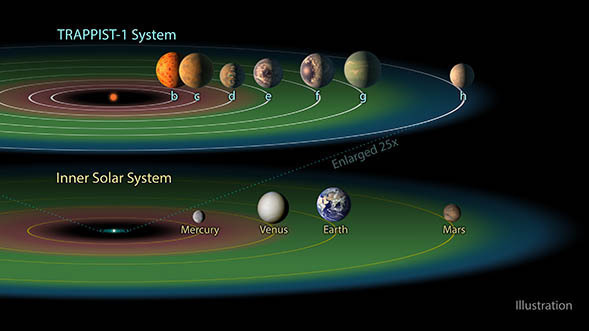
Comparing the TRAPPIST-1 system to the solar system. From http://www.spitzer.caltech.edu/images/6294-ssc2017-01h-The-TRAPPIST-1-Habitable-Zone.
In astronomy, when you look for evidence supporting a hypothesis and don’t find it, that’s called a “null result“. The null result is usually not all that exciting, but last week, an attempt to detect the atmospheres of potentially habitable exoplanets came up null, and that, as it turns out, may mean the planets are habitable.
In a recent study published last week in Nature Astronomy, Dr. Julien de Wit of MIT and colleagues observed the transits of four of the planets in the TRAPPIST-1 system. The discovery of this system was announced last year and generated a lot of interest — it comprises seven Earth-sized planets orbiting a red-dwarf star, and at least four of the planets orbit in the star’s habitable zone. So astronomers are scrambling to determine the climatic conditions on these planets and find out whether they host life.
Key to those conditions is the composition of the planets’ atmospheres, and the best way to probe atmospheres lightyears distant is to detect the colors of the planets’ shadows as they pass in front of their host stars, i.e. as they transit. When light from the star passes through a planet’s atmosphere, the cool gases can imprint spectral signatures, which we can then detect using a very sensitive telescope — de Wit used the Hubble Space Telescope.
Now, even though the TRAPPIST planets are Earth-sized, that doesn’t mean their atmospheres are Earth-like — astronomers have founds lots of weird planets in the last several years. The atmospheres could be hydrogen-rich like Jupiter, hydrocarbon-rich like Neptune, or rich in nitrogen and oxygen like Earth.
In principal, each kind of atmosphere would give a distinct spectrum, but in practice, atmospheres rich in hydrocarbons or nitrogen, potentially good atmospheres for life, are difficult to detect because they are weighty and drape over the planet like a heavy blanket. By contrast, a hydrogen-rich atmosphere, although probably not great for life, can be light and fluffy, relatively easy to detect.
When de Wit and colleagues analyzed transit data they collected from Hubble showing transits for planets TRAPPIST-1 d, e and f, they found no atmospheric signals down to their detection limits. The spectra below show this lack of atmospheric coloration and what they would have detected if the atmosphere was hydrogen-rich.
Now, of course, this non-detection does NOT mean the planets are habitable or even Earth-like. As the figure shows, their atmospheres could still be radically different from the Earth’s (drenched in water vapor or carbon dioxide-rich like Venus), but it rules out the possibility that they are Jupiter-like — potentially good news for life there.
Very likely, when the James Webb Space Telescope finally launches next year, the TRAPPIST-1 system will be one of its first targets. JWST’s vastly improved sensitivity will help reveal not just a potent null result for the TRAPPIST-1 system but may also reveal the glimmer of distant Earth-like worlds.
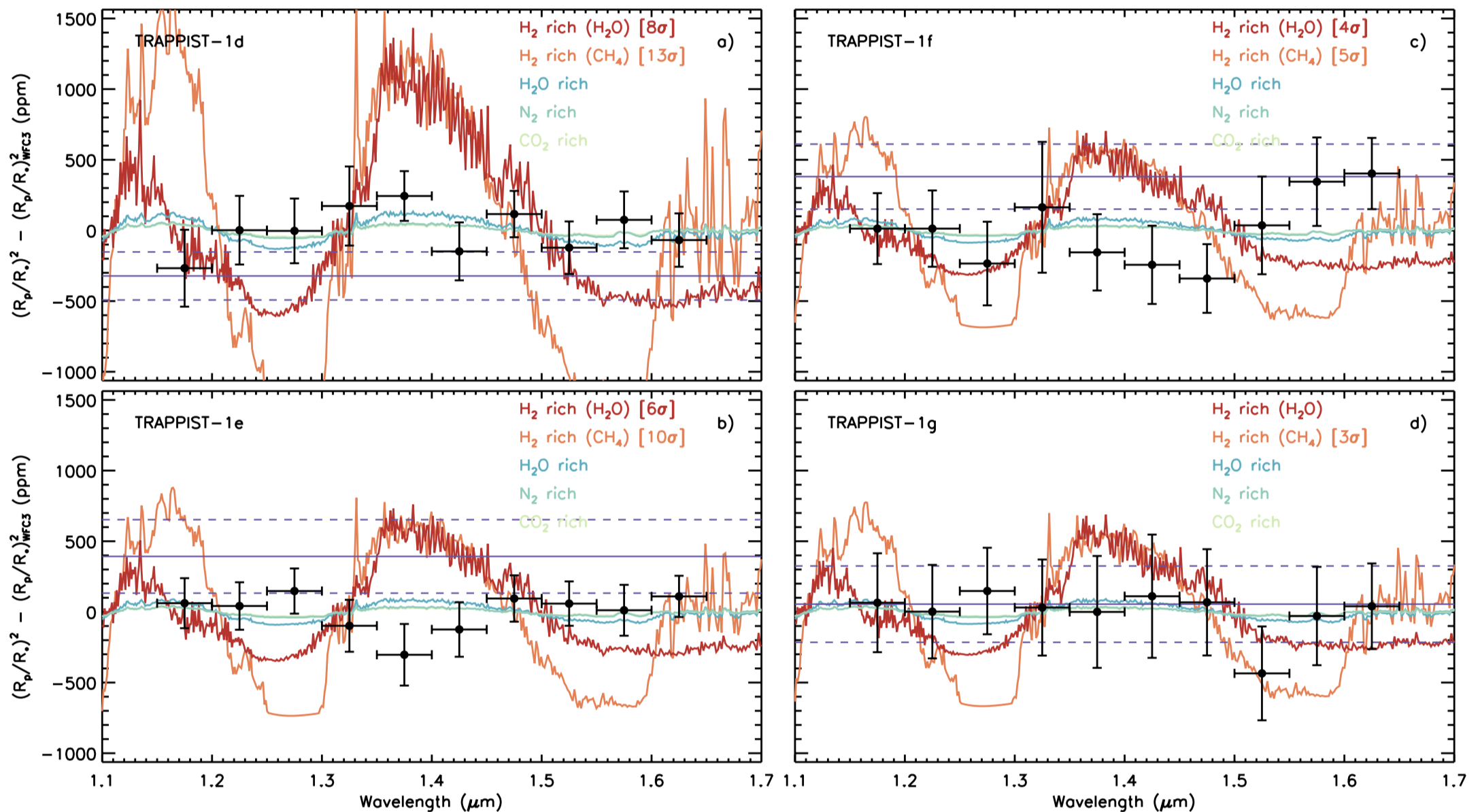
Spectra for TRAPPIST-1 d, e, f, and g. From de Wit et al. (2018) – https://www.nature.com/articles/s41550-017-0374-z.
 Unless you were living under a very large and heavy rock last week, you probably heard about the discovery of seven planets in the TRAPPIST-1 system by Michaël Gillon and colleagues.
Unless you were living under a very large and heavy rock last week, you probably heard about the discovery of seven planets in the TRAPPIST-1 system by Michaël Gillon and colleagues.
Although this system was already known to host three, roughly Earth-sized transiting planets, the discovery of four more throws the door wide open for habitability – all seven planets receive the right amount of starlight from their diminutive red-dwarf host that liquid water might be stable on their surfaces.
There are so many interesting questions to explore for this system – What are the planets’ atmospheres like? How did this system of tightly-packed planets form and how do their orbits remain stable? And, of course, are they habitable?
Fortunately, concerted follow-up observations and theoretical studies can probably a lot of these questions. The fact that the planets all transit their small host star means their atmospheres are ideal for study by the James Webb Space Telescope. Strong gravitational tugs among the planets caused their orbits to change visibly over the course of the observations, so we have strong constraints on how exactly the planets interact.
The last and probably most important question is going to be a lot more difficult to answer. But since a detailed understanding of this system is likely (and probably inevitable, given the enormous enthusiasm for this system), we’ll soon be very close to answering the question of whether the TRAPPIST-1 system is habitable and maybe even inhabited.
One bit of trivia: the TRAPPIST survey that discovered this system was named in honor of the contemplative Roman Catholic religious order of Trappists, and the astronomers reportedly celebrated their discovery with a round of Trappist beer. Maybe this should be the start of a new tradition of naming new planetary systems after beers.

The tightly packed system, named Kepler-444, is home to five small planets in very compact orbits. The planets were detected from the dimming that occurs when they transit the disc of their parent star, as shown in this artist’s conception. From http://www.nasa.gov/ames/kepler/astronomers-discover-ancient-system-with-five-small-planets/.
In journal club on Friday, we discussed a fascinating paper from Campante and colleagues announcing discovery of one of the oldest planetary systems ever discovered — Kepler-444. The system comprises five planets, ranging from roughly Mercury- to Venus-sized with orbital periods from about 3 to 9 days.
Studying the frequencies of oscillations within the K-dwarf host star (an approach known as asteroseismology), Campante et al. estimate the host star, and therefore probably the planets, is about 11 billion years old, almost as old as the Milky Way galaxy itself.
To put that age into perspective, by the time our solar system formed, about 5 billion years ago, the Kepler-444 was already a billion years older than our solar system is now.
The existence of such an old system tells us that rocky planets began forming almost as soon as the Milky Way itself formed, which allows for the exciting possibility of very ancient life in the galaxy.
Present at journal club were Jennifer Briggs, Trent Garrett, Nathan Grisgby, Emily Jensen, Liz Kandziolka, Brenton Peck, and Jacob Sabin.

Mechanical failures interrupted Kepler’s original mission, but the telescope is still hunting exoplanets. From http://www.nature.com/news/three-super-earth-exoplanets-seen-orbiting-nearby-star-1.16740.
Discussed a brilliant paper today in journal club from Ian Crossfield and collaborators, in which they announce the discovery of a three-planet system around a nearby M-dwarf star.
The team found the new system in data from the re-incarnated Kepler mission called K2. This system is only the second discovered by the mission (the first was announced a few months ago).
This new system is especially exciting because, as the authors point out, it is observable by other available facilities, allowing astronomers to characterize the planets and star in detail.
The outermost planet in the system, with an orbital period of 45 days, is very near the inner edge of the system’s habitable zone and has a temperature of about 310 K (100 F), making it plausibly habitable. Combined with the fact that we can probably characterize the planet in detail, there’ll probably be a flurry of exciting studies of the system very soon.
Journal club was attended by Jennifer Briggs, Trent Garrett, Nathan Grigsby, Emily Jensen, Liz Kandziolka, and Brenton Peck.